RSA加密技术在Linux操作系统中的应用-rsalinux (rsa加密技术的特点是)

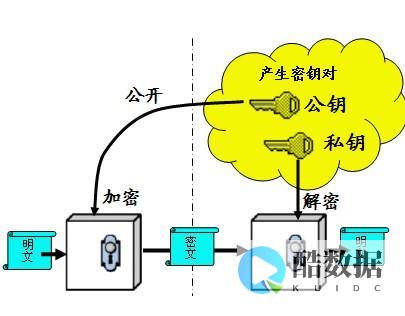
RSA加密技术是目前最常用的一种特种加密技术，它引入了公钥系统，可以有效地抵御外来的破坏并且安全的实现信息传输。RSA加密技术在Linux操作系统中得到了广泛的应用，下面将具体介绍一下RSA加密技术如何应用在Linux操作系统中。

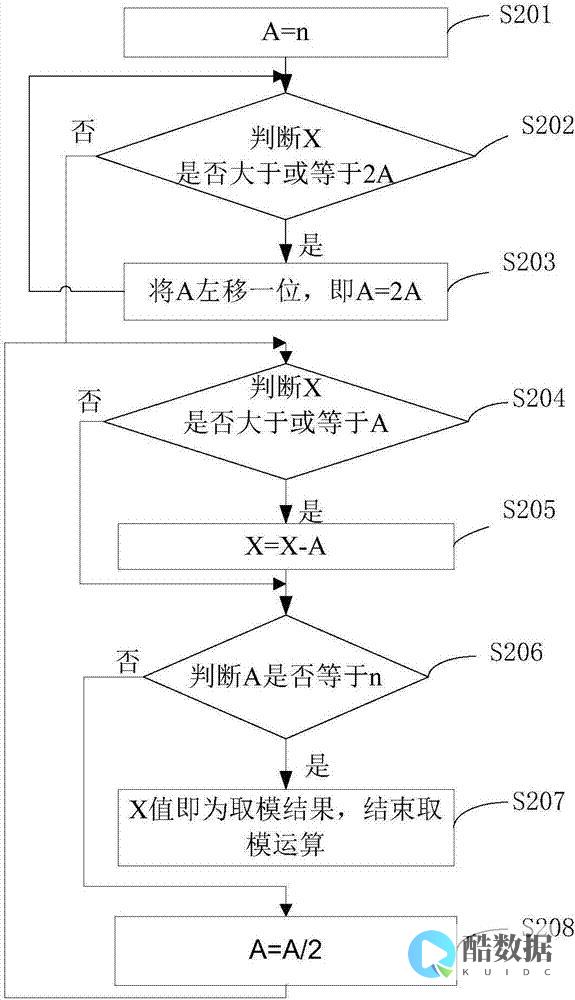
RSA加密技术在Linux操作系统中主要用于加密用户账户和 服务器 之间的通信，以确保数据的安全性和保护隐私。首先，用户在安装Linux操作系统的时候需要双方确定一个秘钥，用私钥进行加密，用公钥把加密信息发给另一方。双方认证后，用户在和服务器通信时，信息发送方会对数据加上一个签名码，信息接收方收到消息后用私钥验证，最终达到信息安全传输的目的。

RSA加密技术常用的实现应用是在Linux终端下使用Openssl工具，首先我们应当在终端安装OpenSSL：

# apt-get install openssl

然后我们可以输入以下命令生成RSA私钥：

# openssl genrsa -aes256 -out private.pem 4096

生成的私钥会保存在private.pem文件中，然后我们可以使用以下命令生成公钥：

# openssl rsa -in private.pem -outform PEM -pubout -out public.pem

生成的公钥会保存在public.pem文件中。此外，我们还可以使用以下命令将信息进行加密：

# openssl rsautl -encrypt -inkey public.pem -pubin -in message.txt -out message.enc

一旦加密后，我们就可以使用私钥来解密这个消息：

# openssl rsautl -decrypt -inkey private.pem -in message.enc -out message.dec

以上就是RSA加密技术如何在Linux操作系统中进行应用的介绍，它的应用不仅可以让传输的数据更安全，还可以保护用户的隐私。

香港服务器首选树叶云，2H2G首月10元开通。树叶云（www.IDC.Net）提供简单好用，价格厚道的香港/美国云服务器和独立服务器。IDC+ISP+ICP资质。ARIN和APNIC会员。成熟技术团队15年行业经验。

如何使用公钥/私钥登入 Linux 系统

RSA加密与对称加密如何使用呢？他们的混合应用又应该怎么用呢？

RSA算法是第一个能同时用于加密和数字签名的算法。 RSA算法能生成公私钥对。 假设A、B要通信，那么他们需要彼此知道对方的公钥，如果a向b发送信息，a先用自己的私钥对信息进行加密（即签名），然后用b的公钥进行加密。 当 b收到消息时，先用自己的私钥进行解密，然后用a的公用进行解密（即验证签名），即可看到a发送的明文信息。 若是用对称密钥进行加密，则双方公用一个密钥，这个密钥需要绝对保密，不能让别人知道。 a在向b发送信息前，先用这个密钥对信息进行加密，然后把加密的信息发送给b，之后再把密钥通过另一通道发送给b(要保证密钥传输的安全，不被其他人截获)，b收到密文和密钥后，再用这个密钥进行解密，就可以得到原文。 若混合使用，假设还是a向b发送信息，a先用自己的私钥进行签名，然后再用双方公用的对称密钥（即会话密钥）进行加密，得到加密后的密文，然后用b的公钥对双方的会话密钥进行加密，得到加密的会话密钥，然后把加密的密文和加密的会话密钥一起发给b，b收到后先用自己的私钥对加密的会话密钥进行解密，得到会话密钥，再用会话密钥对加密的密文进行解密，得到签名的信息，然后用a的公钥对签名进行验证，便可得到原始信息。

如何使用16进制编码的RSA公钥进行RSA加密

我们来回顾一下RSA的加密算法。 我们从公钥加密算法和签名算法的定义出发，用比较规范的语言来描述这一算法。 RSA公钥加密体制包含如下3个算法：KeyGen（密钥生成算法），Encrypt（加密算法）以及Decrypt（解密算法）。 (PK,SK)\leftarrowKeyGen(\lambda)。 密钥生成算法以安全常数\lambda作为输入，输出一个公钥PK，和一个私钥SK。 安全常数用于确定这个加密算法的安全性有多高，一般以加密算法使用的质数p的大小有关。 \lambda越大，质数p一般越大，保证体制有更高的安全性。 在RSA中，密钥生成算法如下：算法首先随机产生两个不同大质数p和q，计算N=pq。 随后，算法计算欧拉函数\varphi(N)=(p-1)(q-1)。 接下来，算法随机选择一个小于\varphi(N)的整数e，并计算e关于\varphi(N)的模反元素d。 最后，公钥为PK=(N,e)，私钥为SK=（N,d）。 CT\leftarrowEncrypt(PK,M)。 加密算法以公钥PK和待加密的消息M作为输入，输出密文CT。 在RSA中，加密算法如下：算法直接输出密文为CT=M^e\mod\varphi(N) M\leftarrowDecrypt(SK,CT)。 解密算法以私钥SK和密文CT作为输入，输出消息M。 在RSA中，解密算法如下：算法直接输出明文为M=CT^d\mod\varphi(N)。 由于e和d在\varphi(N)下互逆，因此我们有：CT^d=M^{ed}=M\mod\varphi(N) 所以，从算法描述中我们也可以看出：公钥用于对数据进行加密，私钥用于对数据进行解密。 当然了，这个也可以很直观的理解：公钥就是公开的密钥，其公开了大家才能用它来加密数据。 私钥是私有的密钥，谁有这个密钥才能够解密密文。 否则大家都能看到私钥，就都能解密，那不就乱套了。 =================分割线================= 我们再来回顾一下RSA签名体制。 签名体制同样包含3个算法：KeyGen（密钥生成算法），Sign（签名算法），Verify（验证算法）。 (PK,SK)\leftarrowKeyGen(\lambda)。 密钥生成算法同样以安全常数\lambda作为输入，输出一个公钥PK和一个私钥SK。 在RSA签名中，密钥生成算法与加密算法完全相同。 \sigma\leftarrowSign(SK,M)。 签名算法以私钥SK和待签名的消息M作为输入，输出签名\sigma。 在RSA签名中，签名算法直接输出签名为\sigma=M^d\mod\varphi(N)。 注意，签名算法和RSA加密体制中的解密算法非常像。 b\leftarrowVerify(PK,\sigma,M)。 验证算法以公钥PK，签名\sigma以及消息M作为输入，输出一个比特值b。 b=1意味着验证通过。 b=0意味着验证不通过。 在RSA签名中，验证算法首先计算M=\sigma^e\mod\varphi(N)，随后对比M与M，如果相等，则输出b=1，否则输出b=0。 注意：验证算法和RSA加密体制中的加密算法非常像。 所以，在签名算法中，私钥用于对数据进行签名，公钥用于对签名进行验证。 这也可以直观地进行理解：对一个文件签名，当然要用私钥，因为我们希望只有自己才能完成签字。 验证过程当然希望所有人都能够执行，大家看到签名都能通过验证证明确实是我自己签的。 =================分割线================= 那么，为什么题主问这么一个问题呢？我们可以看到，RSA的加密/验证，解密/签字过程太像了。 同时，RSA体制本身就是对称的：如果我们反过来把e看成私钥，d看成公钥，这个体制也能很好的执行。 我想正是由于这个原因，题主在学习RSA体制的时候才会出现这种混乱。 那么解决方法是什么呢？建议题主可以学习一下其他的公钥加密体制以及签名体制。 其他的体制是没有这种对称性质的。 举例来说，公钥加密体制的话可以看一看ElGamal加密，以及更安全的Cramer-Shoup加密。 签名体制的话可以进一步看看ElGamal签名，甚至是BLS签名，这些体制可能能够帮助题主更好的弄清加密和签名之间的区别和潜在的联系。 至于题主问的加密和签名是怎么结合的。 这种体制叫做签密方案（SignCrypt），RSA中，这种签密方案看起来特别特别像，很容易引起混乱。 在此我不太想详细介绍RSA中的加密与签字结合的方案。 我想提醒题主的是，加密与签字结合时，两套公私钥是不同的。